凹凸の法則の誤りとは？”滑り”は患者の反応を確認しながら適時調整！

モビライゼーションとは

リズミカルで反復的な受動的な動きを患者の許容範囲、また、随意・副運動の範囲で行い、痛みのない完全な関節機能を回復することを目的とした受動的な技術です。

[st-cmemo myclass="st-text-guide st-text-guide-sankou" fontawesome="fa-quote-left" iconcolor="#919191" bgcolor="#fafafa" color="#000000" bordercolor="" borderwidth="" iconsize=""]

Mobilization

Passive techniques designed to restore a full painless joint function by rhythmic, repetitive passive movements to the patients’ tolerance, in voluntary and/or accessory ranges.

（Cook, Chad E.. Orthopedic Manual Therapy (p.526). Pearson Education）

[/st-cmemo]

関節に行う場合、関節モビライゼーションと呼ばれるのが一般的です。

関節モビライゼーションの方法はメソッドによって異なりますが、知っておきたい基本知識がいくつかあります。

今回は、凹凸の法則について考えたいと思います。

凹凸（おうとつ）の法則（concave convex rule）

いわずと知れた凹凸の法則です。

関節包内運動を理解するのに役立つ法則ですが、当てはまらないことも指摘されています。

書籍によっては、凹凸の法則が当てはまらないケースについて述べていないこともあり注意が必要です。

関節包内では、転がり、滑り、軸回旋といった基本的な動きがあります。

２つの骨をつつむ関節包の内側では、”転がり” と ”滑り” という動きが同時に起こっています。

この滑りと転がりの運動の法則を凹凸の法則といいます。

[st-cmemo fontawesome="fa-file-text-o" iconcolor="#919191" bgcolor="#fafafa" color="#000000" bordercolor="" borderwidth="" iconsize=""]英語では、凹のことをconcave、凸のことをconvex と言います。concave は凹？凸？になることがあり、conCaveはCだから凹、conVex は Vでとがっているから凸と形で覚えた単語です。ちなみに、“でこぼこ”という日本語をワードで変換すると、凸凹になります。”おうとつ”は、凹凸です。[/st-cmemo]

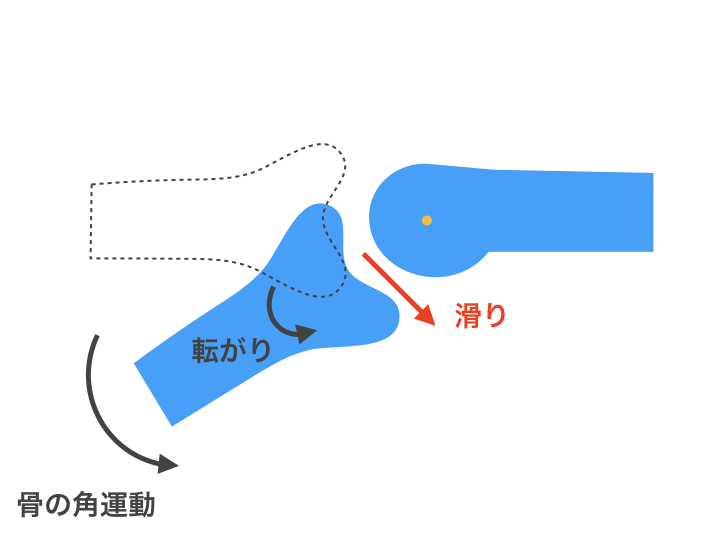
凹の法則

凹の法則・・・凹の関節面が動く時には転がりと滑りの方向は同じになります。

例）膝関節の屈曲：凹 大腿骨 凸 脛骨

脛骨は下方向に動きます（骨運動）。関節内の動きでも、脛骨は下方向に滑ります （＊ただし、凹凸の法則に従えばの話です。後述の「凹凸の法則は完璧な法則ではない！」を読んでください）。

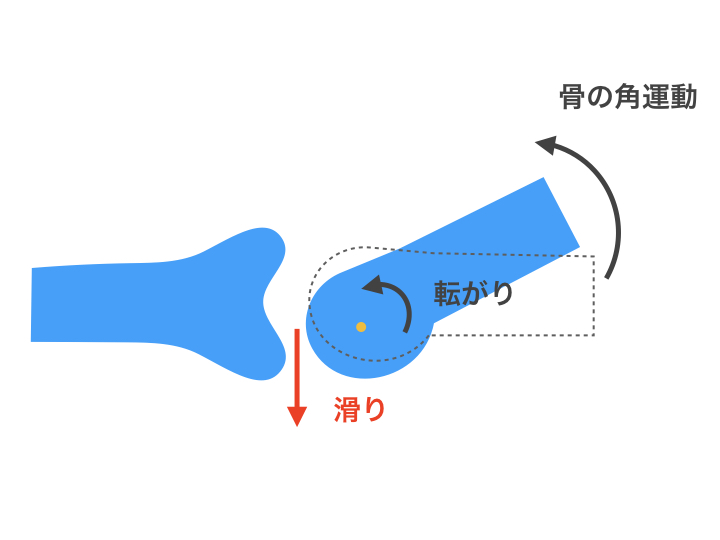
凸の法則

凸の法則・・・凸の関節面が動く時には転がりと滑りの方向は逆になります。

例）肩関節の外転運動：凹 肩甲骨 凸 上腕骨

上腕骨は上方向に動きます（骨運動）が、関節内の動きでは上腕骨頭が下方向に滑ります。

関節機能不全

何かしらの原因（関節内での炎症・癒着など）によって、関節機能に問題が起こります。

関節包が緊張し、”滑り”が減り、”転がり”の動きになる結果、関節面の圧迫が生じて疼痛が誘発されます。

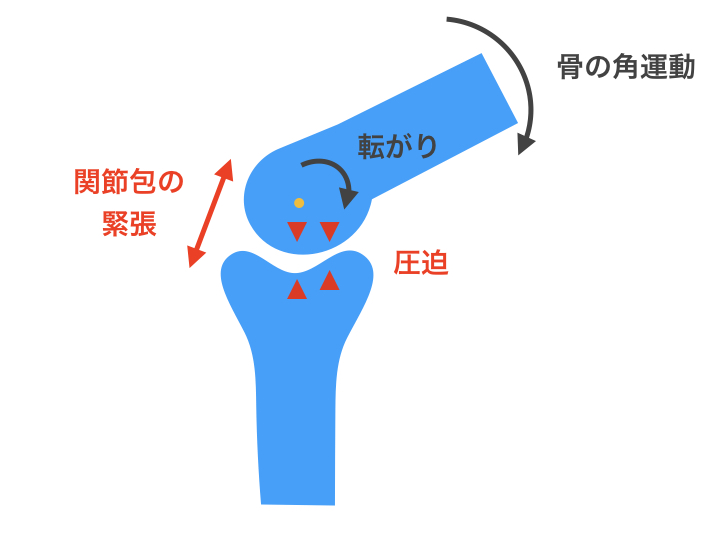
そのため、関節内の動きを改善するために”滑り”の動きをだす必要があります。

（ただし、滑りだけでなく、"転がり”の動きを重要視するメソッドもあります。）

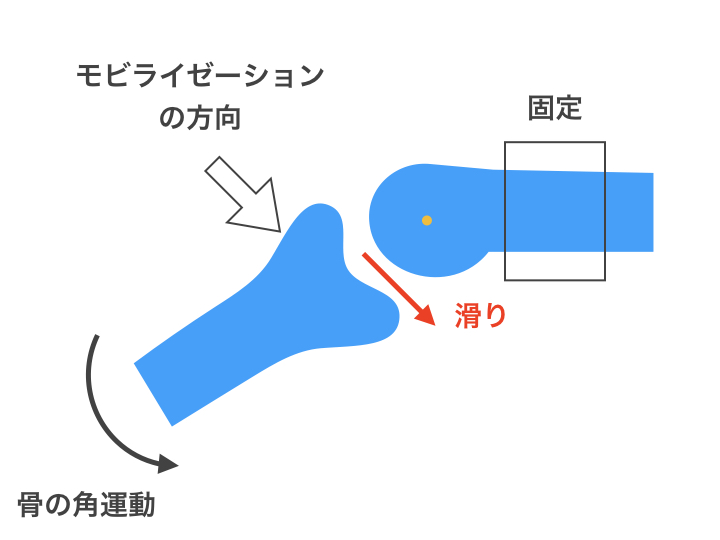
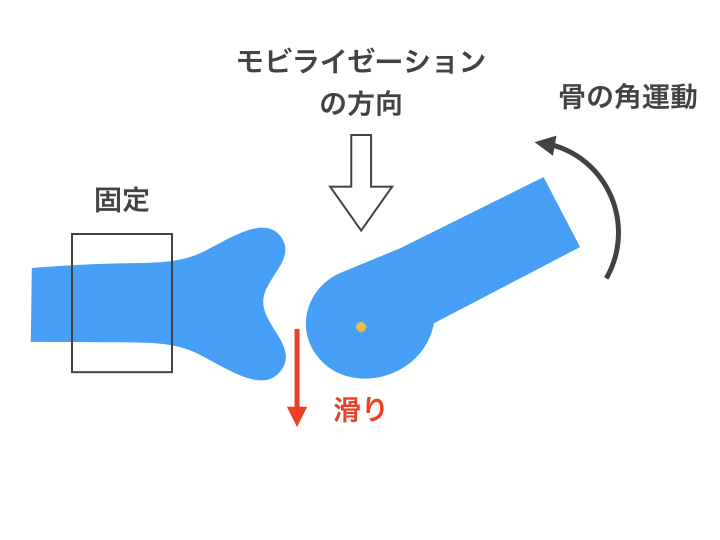
関節モビライゼーションと滑りの方向

関節包内運動の異常がある場合、関節に対して“滑り”を加えるのが基本的な関節モビライゼーションの考え方です。

関節モビライゼーションでは、凹凸の法則を参考にすることが多いです（＊ただし、凹凸の法則に従わない場合があります。後述の「凹凸の法則は完璧な法則ではない！」を読んでください）。

滑りの力は治療する関節の治療面（凹）を平行に動かす、また、治療面に対して凸を平行に動かします。

（治療面（Treatment plane）は常に、凹の関節面をいいます）

可能な限り前腕の向きと滑りの力の方向を一致させるのが基本ですね。

関節に対して、平行ではないと効果半減、また、ぶつかって圧迫ストレスを生じるので注意が必要です。

凹凸の法則で挙げた２つの例を考えてみましょう。

例１）膝蓋大腿関節

例２）肩甲上腕関節

凹凸の法則は完璧な法則ではない！

凹凸の法則は、関節運動を考える上で基本となるものですが、完璧ではありません。

市川（2007）、Neumann DA（2012）らは、凹凸の法則の欠陥を指摘しています。

凹凸の法則に当てはまらない例として、膝関節屈曲、肩関節の外旋などがあります。

膝関節の場合、凹凸の法則に従えば屈曲に伴い脛骨は後方に滑っていきます。

しかし、実際は、転がりと滑り（回旋）により脛骨関節面の後方と大腿骨が接することで深い屈曲を可能にしていて、転がりの分だけ脛骨は後方ではなく前方に移動しています。

膝関節深屈曲を獲得する場合は、脛骨を前方かつやや下方に誘導すると曲がってくることが多いですね。

肩関節の場合、理論上、肩関節外旋時に上腕骨頭が後方に転がり前方に滑ります。

しかし、後方組織が硬くなってしまった場合、上腕骨頭を後方から前方へ押し出してしまい、前方組織への圧迫ストレスを増大させます。Obligate translation というキーワードでいろいろと議論されています。

後方組織の短縮がある肩では、肩関節外旋時（自動および他動運動）に疼痛が誘発された場合、上腕骨頭を後方に押し込みながら再度、外旋すると疼痛消失・可動域増大が認められることが多いです。

脊椎の椎間関節はどうでしょうか？

脊椎の椎間関節の関節面は個体差があるので、凹凸の法則というよりも、関節面の滑りの方向が重要になります。

脊椎は部位によって矢状面での関節面の角度が異なります（頸椎：45°、胸椎：60°、腰椎：90°）。

立位・座位で滑りの力を加える場合は、矢状面での関節面の角度を考慮する必要があります。

患者の反応を見逃してはならない

さて、凹凸の法則ですが関節包内運動の動きをざっくり理解する、モビライゼーションの方向を考えることには適していますが、誤りも指摘されていることを述べました。

凹凸の法則、凹凸の法則の誤りについて述べましたが、患者の反応も重要です。

例えば、膝関節屈曲時に脛骨が前方に滑るという話をしましたが、患者の状態によって異なります。

患者によっては脛骨内旋の滑りがいい場合もあります。

マリガンコンセプトを適用するならば、外側・内側グライドが効果的な場合もあります。

当たり前ですが、脛骨大腿関節以外の関節も考慮する必要があります。膝関節の場合は、膝蓋大腿関節、近位脛腓関節ですね。

骨の位置、軟部組織の状態、患者の反応などを考慮して、適時、滑りの方向を調整することが重要ですね。

[st-cmemo myclass="st-text-guide st-text-guide-attention" fontawesome="fa-exclamation-circle" iconcolor="#ef5350" bgcolor="#ffebee" color="#000000" bordercolor="#ffcdd2" borderwidth="" iconsize=""]本記事では関節に焦点を当てています。膝関節屈曲についても、他動運動と自動運動の制限、自動運動の制限＋疼痛、荷重下でのしゃがみこみ時の疼痛、また、疼痛においても、膝前面の疼痛、膝窩の疼痛などさまざまなケースがあり、それぞれ対応が異なります。四肢に関しては軟部組織が原因となっていることも多々有り、また、軟部組織に影響を与える姿勢や動作、生活習慣の改善も大事です。[/st-cmemo]

参考文献・書籍

市橋則明：凹凸の法則に従った関節可動域運動は間違いである, 2007

Neumann DA：The Convex-Concave Rules of Arthokinematics: Flawed Just Misinterpreted?, 2012

藤縄：徒手的理学療法, 三輪書店, 2009

関連する書籍の紹介

2011年に第２版が出版、Kindele 版が安いです。